Articulo especial
Cálculo de tamaño muestral y precisión para estudios epidemiológicos:
desarrollo e implementación del paquete CalculadoraPrevalencia
en R
Sample size and precision calculation for
epidemiological studies: development and implementation of the CalculadoraPrevalencia,
an R package
Víctor Juan Vera-Ponce1,a
- Universidad Nacional Toribio Rodríguez de
Mendoza de Amazonas, Amazonas, Perú.
- Médico cirujano.
ORCID: https://orcid.org/0000-0003-4075-9049
CORREO: vicvepo@gmail.com
Fiorella E. Zuzunaga-Montoya2,b
- Universidad Continental, Lima, Perú.
- Médico cirujano.
ORCID: https://orcid.org/0000-0002-2354-273X
CORREO: fiorellazuzunaga@gmail.com
Christian Humberto Huaman-Vega1,c
- Universidad Nacional Toribio Rodríguez de
Mendoza de Amazonas, Amazonas, Perú.
- Estudiante de Psicología.
ORCID: https://orcid.org/0000-0003-2333-2254
CORREO: 7497550991@untrm.edu.pe
Nataly Mayely Sanchez-Tamay1,d
- Universidad Nacional Toribio Rodríguez de
Mendoza de Amazonas, Amazonas, Perú.
- Estudiante de Medicina.
ORCID: https://orcid.org/0009-0003-5951-4196
CORREO: natalymayely@gmail.com
Carmen Inés Gutierrez de
Carrillo1,e
- Universidad Nacional Toribio Rodríguez de
Mendoza de Amazonas, Amazonas, Perú.
- Médico cirujano.
ORCID: https://orcid.org/0000-0002-4711-7201
CORREO: carmen.gutierrez@untrm.edu.pe
Corresponsal:
Víctor Juan Vera-Ponce
CORREO: vicvepo@gmail.com
Citar como: Vera-Ponce VJ, Zuzunaga-Montoya FE, Huaman-Vega CH, Sanchez-Tamay NM,
Gutierrez de Carrillo CI. Cálculo de tamaño muestral y precisión para estudios epidemiológicos:
desarrollo e implementación del paquete CalculadoraPrevalencia
en R. Rev Perú Cienc
Salud. 2025;7(2):143-50. doi: https://doi.org/10.37711/rpcs.2025.7.2.4
RESUMEN
La determinación del tamaño muestral
y la evaluación de precisión son elementos cruciales en investigación
epidemiológica. Este artículo presenta CalculadoraPrevalencia,
una herramienta en R que facilita estos cálculos incorporando aspectos
metodológicos y logísticos. La calculadora maneja diversos escenarios:
poblaciones finitas e infinitas, estratificación y ajustes por
sensibilidad/especificidad de instrumentos. Mediante ejemplos prácticos en
diferentes contextos (población urbana infinita, población rural finita,
muestreo universitario estratificado y análisis de datos existentes), se
demuestra su aplicabilidad. La herramienta integra consideraciones logísticas,
calculando sujetos a contactar según tasas de rechazo/elegibilidad y estimando
tiempos de trabajo de campo. Su versatilidad facilita tanto la planificación
prospectiva como la evaluación de datos existentes, mientras que la innovadora
incorporación de aspectos logísticos proporciona una visión realista de los
recursos necesarios para estudios epidemiológicos exitosos.
Palabras clave: muestreo; tamaño de
la muestra, muestreo estratificado; muestreo aleatorio; muestreo
sistemático.
ABSTRACT
Determining
sample size and assessing precision are essential components of epidemiological
research. This article presents CalculadoraPrevalencia, an R-based tool designed to
facilitate these calculations by incorporating both methodological and
logistical factors. The calculator supports various scenarios, including finite
and infinite populations, stratified sampling, and adjustments for instrument
sensitivity and specificity. Its utility is demonstrated through practical
examples across diverse contexts: infinite urban populations, finite rural
populations, stratified university sampling, and the analysis of existing
datasets. The tool also addresses logistical considerations, estimating the
number of subjects to contact based on rejection and eligibility rates, and
projecting expected fieldwork duration. Its versatility enables both
prospective planning and retrospective data evaluation, while the innovative
inclusion of logistical components offers a realistic perspective on the
resources needed to carry out successful epidemiological studies.
Keywords:
sampling;
sample size; stratified sampling; random sampling; systematic sampling.
INTRODUCCIÓN
El cálculo del tamaño muestral
constituye un elemento decisivo en toda investigación científica, representando
una decisión crítica que determina la capacidad para obtener resultados
precisos y significativos, con impacto directo en la validez y viabilidad del
proyecto (1,2).
Su importancia fundamental radica en controlar los
errores inherentes a la investigación. Un cálculo adecuado mantiene estos
errores en niveles aceptables, proporcionando el poder estadístico necesario
para detectar diferencias significativas cuando realmente existen, aspecto
crucial para la validez de los resultados (3). Contrariamente a la
intuición común, un mayor tamaño poblacional no necesariamente requiere una
muestra proporcionalmente más grande, pues el tamaño muestral
se determina principalmente por la magnitud de las proporciones a detectar y la
precisión deseada (4).
En esta revisión presentamos los conceptos
fundamentales del cálculo muestral e introducimos una
calculadora desarrollada por nuestro equipo, que incorpora funciones
frecuentemente ignoradas por otras herramientas, incluyendo un componente
logístico que facilita la evaluación de la factibilidad temporal, garantizando
tanto el rigor científico como la viabilidad práctica de los estudios
epidemiológicos.
Conceptos fundamentales para el
cálculo de tamaño muestral
El cálculo del tamaño muestral
en estudios de prevalencia requiere la comprensión de varios conceptos
estadísticos fundamentales que se describen a continuación.
Proporción o prevalencia esperada
Representa la frecuencia anticipada del evento de
interés en la población de estudio, expresándose como un valor entre 0 y 1. Por
ejemplo, una prevalencia esperada de 0,20 indica que esperamos encontrar el
evento en el 20 % de la población estudiada. Justamente, aquí surge una
aparente paradoja: debemos anticipar lo que esperamos encontrar antes de
realizar el estudio. Esta situación, aunque desafiante, puede abordarse
mediante diferentes estrategias metodológicas (5).
Existen tres aproximaciones principales para resolver
esta aparente paradoja. La primera consiste en recurrir a la literatura
existente, utilizando información de estudios similares previos como
referencia. La segunda implica preguntar a los expertos del campo sobre cuál
sería esa proporción que posiblemente obtengamos al realizar el estudio. La
tercera aproximación, particularmente valiosa, es la realización de un estudio
piloto (6).
Finalmente, el estudio piloto emerge como una
herramienta metodológica invaluable que trasciende el mero cálculo del tamaño muestral. A través del piloto, podemos evaluar la
efectividad del proceso de reclutamiento, verificar la calidad de las
mediciones propuestas y anticipar posibles desafíos en el seguimiento de los
participantes, incluyendo la estimación de potenciales pérdidas durante el
estudio. Aunque no existe un consenso claro, se ha señalado en la literatura
existente que una muestra piloto mínima sería de 30 observaciones.
Sin embargo, en situaciones donde no se tiene una
estimación previa confiable es común utilizar una prevalencia de 0,5, lo que
resulta en el máximo tamaño muestral posible,
asegurando así una muestra suficiente independientemente de la prevalencia
real.
Nivel de confianza
El nivel de confianza es otro concepto esencial que
representa la probabilidad de que el intervalo de confianza calculado contenga
el verdadero valor poblacional. Típicamente se establece en 0,95 (95 %) o 0,99
(99 %). Este valor refleja nuestra certeza estadística: con un nivel de
confianza del 95 % podemos afirmar que, si repitiéramos el estudio múltiples
veces, en el 95 % de las ocasiones el intervalo calculado contendría el
verdadero valor poblacional. Al igual que con la precisión, un mayor nivel de
confianza requiere un mayor tamaño muestral (7).
Precisión
La precisión y el nivel de confianza son conceptos
fundamentales que determinan la calidad de las estimaciones en estudios de
prevalencia. Mientras el nivel de confianza (típicamente 95 %) indica la
probabilidad de que el parámetro poblacional esté dentro del intervalo
calculado, la precisión determina la amplitud de este intervalo. Por ejemplo,
con una prevalencia del 20 %, una precisión del 5 % genera un intervalo de
15-25 %, mientras que una del 2 % lo reduce a 18-22 %. Una mayor precisión
proporciona estimaciones más exactas para la toma de decisiones y permite
detectar diferencias pequeñas pero relevantes, aunque requiere muestras
considerablemente más grandes (1).
La selección de la precisión debe balancear
necesidades científicas y recursos disponibles, considerando que ambos
parámetros afectan multiplicativamente el tamaño muestral.
En estudios exploratorios podría ser aceptable una precisión del 5-7 %,
mientras que investigaciones definitivas para políticas sanitarias podrían
requerir del 2-3 %. Esta decisión también debe considerar la magnitud del
parámetro: una precisión del 5 % podría ser excesiva para una prevalencia del 1
% pero insuficiente para una del 50 %. Este equilibrio entre precisión,
confiabilidad y factibilidad constituye uno de los aspectos más cruciales en el
diseño de investigaciones epidemiológicas.
Población finita o infinita
La distinción entre población finita e infinita en
el cálculo del tamaño muestral trasciende el simple
tamaño poblacional. Esta decisión metodológica depende de múltiples factores
durante la planificación del estudio. Tradicionalmente, se sugiere el enfoque
de población infinita cuando la muestra representa menos del 5 % de la
población total. Sin embargo, este criterio debe evaluarse junto con los
objetivos de inferencia; si pretendemos generalizar más allá de nuestra
población inmediata, el enfoque de población infinita resulta más apropiado,
incluso en poblaciones relativamente pequeñas (8).
El factor de corrección para población finita (FCF)
resulta crucial en esta decisión, ajustando el tamaño muestral
cuando trabajamos con poblaciones finitas. La fórmula del FCF (√ [(N-n) / (N -
1)]) refleja cómo la proporción muestreada afecta la precisión de nuestras
estimaciones. Cuando la muestra representa una proporción significativa de la
población total, el FCF reduce el tamaño muestral
necesario, reconociendo que cada individuo muestreado proporciona más
información sobre la población total (9).
Cuando trabajamos con poblaciones muy grandes o
buscamos hacer inferencias más amplias, el enfoque de población infinita
permite obtener estimaciones más conservadoras y potencialmente más
generalizables, siendo preferible cuando existe incertidumbre sobre el tamaño
exacto de la población o cuando ésta puede variar durante el estudio. La
elección entre ambos enfoques tiene implicaciones prácticas para la precisión y
eficiencia: usar el enfoque de población finita cuando es apropiado puede
optimizar recursos, mientras que el enfoque infinito favorece la
generalización, debiendo equilibrarse según los objetivos del estudio.
Sensibilidad y especificidad de
la prueba
La sensibilidad y especificidad son parámetros
fundamentales que permiten ajustar el cálculo del tamaño muestral
según la precisión del método de medición que utilizaremos para identificar
nuestro evento de interés. Estos parámetros son especialmente relevantes cuando
no utilizamos el estándar de oro. La sensibilidad representa la capacidad del
método para identificar correctamente los casos positivos verdaderos, mientras
que la especificidad refleja su capacidad para identificar correctamente los
casos negativos verdaderos. Ambos parámetros se expresan como proporciones
entre 0 y 1 (10).
Por ejemplo, si utilizamos un cuestionario validado
para detectar depresión que tiene una sensibilidad de 0,90 y una especificidad
de 0,95 (ya que no es el estándar de oro). Esto significa que nuestro
instrumento detectará correctamente al 90 % de los casos verdaderos de
depresión e identificará correctamente al 95 % de los casos sin depresión.
Estos valores afectan la estimación de la prevalencia real y, por consiguiente,
influyen en el tamaño muestral necesario para obtener
estimaciones precisas (10).
Aplicaciones de estratos
El muestreo estratificado mejora la
representatividad y eficiencia en estudios de prevalencia, al dividir la
población en subgrupos mutuamente excluyentes. Esta estrategia resulta valiosa
cuando existen subgrupos diferenciados con posibles variaciones en la
prevalencia del evento estudiado, como ocurre en contextos universitarios donde
los años académicos constituyen estratos naturales (11).
El efecto del diseño es un parámetro crucial que
ajusta el tamaño muestral para compensar la
complejidad de la estratificación. Un valor mayor a 1 indica la necesidad de
una muestra más grande que en un muestreo simple aleatorio para mantener igual
precisión, debido a la variabilidad adicional introducida (12).
Esta metodología permite generar estimaciones
específicas por subgrupo, facilita la identificación de diferencias entre
estratos y optimiza la eficiencia cuando los estratos son homogéneos
internamente, pero heterogéneos entre sí. Puede implementarse proporcionalmente
(respetando proporciones poblacionales) o desproporcionalmente (sobremuestreando estratos específicos), según los objetivos
y consideraciones prácticas de cada investigación.
Tamaño de muestra versus cálculo
de precisión
En estudios de prevalencia existen dos enfoques
fundamentales: el cálculo del tamaño muestral y el
cálculo de la precisión, cada uno respondiendo a diferentes necesidades
investigativas (13,14).
El cálculo del tamaño muestral,
enfoque tradicional y prospectivo, se utiliza en la fase de planificación. El
investigador parte de parámetros predefinidos (prevalencia esperada, precisión
deseada y nivel de confianza) para determinar cuántos sujetos necesita
estudiar. Este enfoque es útil cuando existe flexibilidad en el reclutamiento y
recursos suficientes.
Por el contrario, el cálculo de la precisión
representa un enfoque retrospectivo, valioso cuando trabajamos con un tamaño de
muestra predeterminado por limitaciones presupuestarias, temporales, de
accesibilidad o al utilizar bases de datos existentes.
Consideraciones logísticas
posteriores al cálculo de tamaño muestral
Una vez determinado el tamaño muestral
teórico necesario para nuestro estudio de prevalencia, es fundamental
considerar los aspectos logísticos que influirán en su implementación práctica.
El tamaño muestral calculado representa el número
final de participantes necesarios para el análisis, pero la realidad del
trabajo de campo implica diversos factores que afectarán el número total de
sujetos que deberemos abordar inicialmente (15,16).
La tasa de rechazo y la tasa de elegibilidad son dos
factores cruciales en la planificación logística. La primera representa la
proporción de personas que, siendo contactadas, decidirán no participar; la
segunda refleja qué porcentaje de contactados cumplirán con nuestros criterios
de inclusión y exclusión. Por ejemplo, si necesitamos 300 participantes
finales, esperamos una tasa de rechazo del 20 % y una tasa de elegibilidad del
80 %, deberemos contactar inicialmente a aproximadamente 470 personas. Estas
estimaciones deben basarse en experiencias previas o estudios piloto.
La capacidad operativa del equipo de investigación
determina cuántos sujetos pueden ser procesados diariamente. Este factor
depende del personal disponible, tiempo necesario para aplicar instrumentos,
disponibilidad de equipos o espacios, y horarios tanto del equipo investigador
como de la población objetivo. El tiempo total necesario para completar el
reclutamiento se calcula considerando todos estos elementos; si necesitamos
contactar a 470 personas y podemos procesar 220 participantes mensuales, el
período se extenderá por aproximadamente dos meses y medio.
Uso y presentación de la
calculadora
La calculadora denominada CalculadoraPrevalencia
ha sido diseñada como una herramienta versátil para el cálculo del tamaño muestral y la precisión en estudios de prevalencia,
implementada en el entorno de programación R. Esta herramienta integra
múltiples aspectos metodológicos que tradicionalmente debían considerarse por
separado, permitiendo un análisis más comprehensivo y ajustado a las
necesidades específicas de cada investigación. El investigador que desee usar
la calculadora solo debe instalar el paquete en R denominado devtools::install_github("VicVePo/CalculadoraPrevalencia").
Una vez completada la instalación, los paquetes
pueden ser cargados en la sesión de R mediante el comando library("CalculadoraPrevalencia"). Este proceso simple de
instalación y carga permite a los investigadores acceder inmediatamente a todas
las funcionalidades de cálculo de tamaño muestral y
planificación logística incluidas en cada paquete, facilitando así el diseño y
planificación de sus estudios epidemiológicos.
La estructura de la calculadora CalculadoraPrevalencia
se basa en una función principal que acepta diversos parámetros según las
características específicas del estudio: prevalencia esperada, precisión
deseada y nivel de confianza para el cálculo del tamaño muestral,
con la flexibilidad de incluir el tamaño poblacional cuando es conocido (N) o
especificar NA para poblaciones infinitas, además de incorporar ajustes por la
calidad de las mediciones mediante parámetros de sensibilidad y especificidad
(modificables según el método utilizado). Y para estudios con muestreo
estratificado permite especificar tanto las proporciones de cada estrato (prop_estratos) como el efecto del diseño (efecto_diseno), ofreciendo así una herramienta
comprehensiva para distintos escenarios de investigación epidemiológica (ver
Figura 1).

Figura 1. Matriz de la calculadora de tamaño de
muestra/precisión en R
La versatilidad de la calculadora se evidencia en su
capacidad para funcionar en dos modos distintos mediante el parámetro
"calcular": el modo "muestra" determina el tamaño muestral necesario dada una precisión deseada, mientras que
el modo "precisión" calcula la precisión esperable con un tamaño muestral predeterminado, permitiendo así su aplicación,
tanto en la planificación prospectiva como en la evaluación de diseños con
restricciones muestrales. Adicionalmente, la
herramienta se complementa con una función para el análisis logístico (logística_estudio_transversal) que traduce el tamaño muestral teórico en requerimientos prácticos, considerando
tasas de rechazo, criterios de elegibilidad y capacidad operativa, para
proporcionar estimaciones realistas del tiempo y recursos necesarios (ver
Figura 2).

Figura 2. Matriz de la sección logística posterior al cálculo
de tamaño muestral en R
Los resultados de la calculadora se presentan en un
formato estructurado que incluye no solo el tamaño muestral
o la precisión calculada, sino también todos los parámetros utilizados en el
cálculo. Esto facilita la documentación del proceso de planificación y permite
una comunicación transparente de las decisiones metodológicas en publicaciones
científicas.
Aplicación de ejemplos
Ejemplo 1: estudio de prevalencia
de síntomas de depresión en la ciudad de Chachapoyas
Para estimar la prevalencia de depresión en adultos
de Chachapoyas (población de 80 000 habitantes), consideramos: prevalencia
esperada del 20 %, precisión del 5 %, confianza del 95 % y utilizando el PHQ-9
(sensibilidad 88 % y especificidad del 92 %). Esto se puede visualizar en la
Figura 3.

Figura 3. Cálculo inicial utilizando la CalculadoraPrevalencia
en R
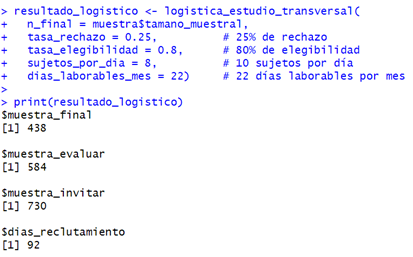
El cálculo indica una muestra necesaria de 438
personas. Considerando una tasa de rechazo del 25 %, elegibilidad del 80 %, y
capacidad para evaluar 8 personas diarias, necesitaremos contactar a 730
personas y planificar 92 días de trabajo de campo. Este cálculo puede verse en
la sección de Anexos (ver Anexo 1).
Ejemplo 2: estudio de prevalencia
de hipertensión arterial en el distrito de Luya
El distrito de Luya (4 200 habitantes) ilustra el
cálculo con población finita. Para este estudio consideramos: prevalencia
esperada del 25 %, precisión del 5 %, confianza del 95 %, utilizando
tensiómetros digitales (sensibilidad del 95 % y especificidad del 92 %). El
cálculo del tamaño muestral se presenta en la Figura
4:

Figura 4. Resultados de cálculo para población finita en Luya
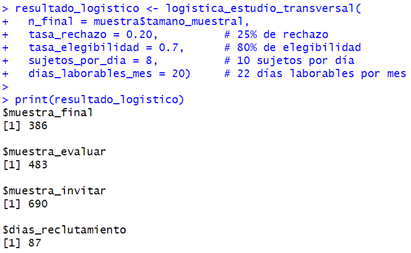
El cálculo indica una muestra de 245 personas, menor
que si consideráramos población infinita (aproximadamente 425), gracias al
factor de corrección finita. Para la planificación logística, con una tasa de
rechazo del 20 %, elegibilidad del 70 % y capacidad para evaluar 6 personas
diarias, necesitaremos contactar a 690 personas durante aproximadamente cuatro
meses. Este cálculo puede verse en el Anexo 2.
El análisis logístico revela que necesitaremos
contactar inicialmente a 690 personas para lograr la muestra calculada. La
implementación del estudio en Luya requerirá aproximadamente cuatro meses de
trabajo de campo, considerando las características geográficas y culturales de
la zona. Es fundamental establecer una estrategia de muestreo que considere la
distribución espacial de la población en el distrito, incluyendo tanto el
centro poblado como los caseríos circundantes, así el muestreo sea no
probabilístico. La coordinación con las autoridades locales y los agentes
comunitarios de salud será crucial para facilitar el acceso a la población y
maximizar la participación.
Ejemplo 3: estudio de prevalencia
de ansiedad en estudiantes de la Universidad Nacional Toribio Rodríguez de
Mendoza de Amazonas con muestreo estratificado
En este estudio universitario fueron consideradas
siete facultades como estratos naturales con sus respectivas proporciones. Se
cuenta con una población estudiantil distribuida en siete facultades con la
siguiente composición: Facultad de Ciencias de la Salud (18,40 %), Facultad de
Ingeniería Civil (17,92 %), Facultad de Ciencias Sociales (14,62 %), Facultad
de Ingeniería de Sistemas (16,51 %), Facultad de Administración (11,32 %),
Facultad de Educación (9,43 %) y Facultad de Ingeniería Agroindustrial (11,80
%). Esperamos una prevalencia de ansiedad del 30 % utilizando el GAD-7
(sensibilidad del 89 % y especificidad del 82 %), con precisión del 5 % y
confianza del 95 % (ver Figura 5).
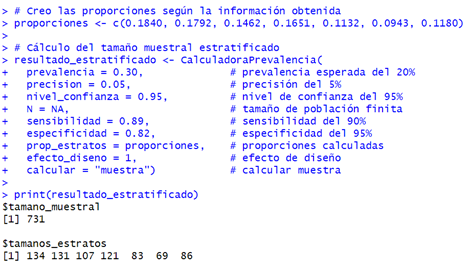
Figura 5. Cálculo del tamaño muestral
estratificado utilizando la CalculadoraPrevalencia en
R
El cálculo nos indica que necesitamos una muestra
total de 402 estudiantes. La estratificación por facultades nos da la siguiente
distribución: 1) Ciencias de la Salud: 134 estudiantes; 2) Ingeniería Civil:
131 estudiantes; 3) Ciencias Sociales: 107 estudiantes; 4) Ingeniería de
Sistemas: 121 estudiantes; 5) Administración: 83 estudiantes; 6) Educación: 69
estudiantes; y 7) Ingeniería Agroindustrial: 86 estudiantes.
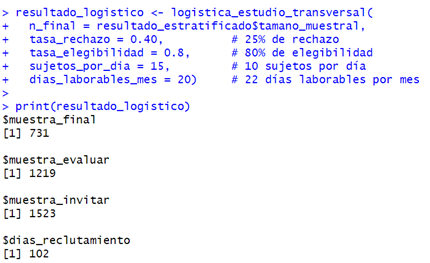
Para el análisis logístico, con una tasa de rechazo
del 40 %, elegibilidad del 80 % y capacidad para evaluar 15 estudiantes
diariamente, necesitaremos contactar inicialmente a 1 523 estudiantes para el
trabajo de campo (ver Anexo 3).
CONCLUSIONES
La planificación metodológica rigurosa es
fundamental para el éxito de los estudios epidemiológicos. La calculadora CalculadoraPrevalencia emerge como una herramienta integral
que facilita no solo el cálculo del tamaño muestral y
la precisión, sino también la consideración de aspectos prácticos cruciales. Su
versatilidad se evidencia al manejar escenarios diversos: poblaciones finitas,
muestras estratificadas y análisis secundarios de datos existentes.
La integración del componente logístico representa
un avance significativo en el diseño de estudios. El cálculo automático del
número total de sujetos a contactar (considerando tasas de rechazo y
elegibilidad) y la estimación del tiempo necesario para el trabajo de campo
permiten una planificación más realista. La incorporación de parámetros como
sensibilidad y especificidad de los instrumentos permite obtener estimaciones
más confiables, ajustadas a cada contexto.
Recomendaciones para el uso
efectivo de la calculadora
En la planificación es crucial evaluar
cuidadosamente los parámetros iniciales. La prevalencia esperada debe basarse
en la literatura previa o en estudios piloto. La precisión deseada debe
equilibrar necesidades científicas con recursos disponibles. La estratificación
debe considerarse cuando existan subgrupos con posibles diferencias en la
prevalencia del evento, aunque esto pueda aumentar la complejidad logística.
Para estudios con pruebas diagnósticas es
fundamental incorporar datos realistas sobre sensibilidad y especificidad,
realizando análisis de sensibilidad cuando estos parámetros no sean conocidos
con certeza. La planificación logística debe ser conservadora en entornos
desafiantes, sobreestimando ligeramente recursos necesarios antes que enfrentar
retrasos significativos.
En análisis secundarios, la evaluación de precisión
debe realizarse antes de los análisis sustantivos. Finalmente, recordemos que
la calculadora es una herramienta de apoyo que no reemplaza el juicio crítico
del investigador. Los resultados deben interpretarse en el contexto específico del
estudio, considerando aspectos prácticos, éticos y científicos, no siempre
reflejados en los cálculos.
REFERENCIAS
1. Mascha EJ, Vetter TR. Significance, Errors, Power, and
Sample Size: The Blocking and Tackling of Statistics. Anesth
Analg. [Internet]. 2018 [Consultado
el 12 de marzo de 2025];126(2):691-8.
doi:10.1213/ANE.0000000000002741
2. Andrade
C. Sample Size and its Importance in Research. Indian J Psychol
Med. [Internet]. 2020 [Consultado el 12 de marzo de 2025];42(1):102-3. doi:10.4103/IJPSYM.IJPSYM_504_19
3. Chow S-C,
Shao J, Wang H, Lokhnygina Y. Sample Size
Calculations in Clinical Research [Internet]. tercera
edición. New York: Chapman and Hall/CRC; 2017 [Consultado el 12 de marzo de
2025]. doi:10.1201/9781315183084
4. Rao UK.
Concepts in sample size determination. Indian J Dent Res [Internet].
2012 [Consultado el 12 de marzo de 2025];23(5):660-4. doi:10.4103/0970-9290.107385
5. Dattalo P. Determining Sample Size [Internet]. Oxford
University Press; 2008 [Consultado el 3 de noviembre de 2024]. doi:10.1093/acprof:oso/9780195315493.001.0001
6. Wang X,
Ji X. Sample Size Estimation in Clinical Research: From Randomized Controlled
Trials to Observational Studies. Chest. [Internet]. 2020 [Consultado
el 3 de noviembre de 2024];158(1S):S12-20.
doi:10.1016/j.chest.2020.03.010
7. Case LD, Ambrosius WT. Power and sample size. Methods Mol Biol. [Internet].
2007 [Consultado el 3 de noviembre de 2024];404:377-408.
doi:10.1007/978-1-59745-530-5_19
8. Charan J, Biswas T. How to calculate sample size for
different study designs in medical research? Indian J Psychol
Med. [Internet]. 2013 [Consultado el 3 de noviembre de 2024];35(2):121-6.
doi:10.4103/0253-7176.116232
9. Population
Correction Factor - an overview | ScienceDirect
Topics [Internet]. [Consultado el 3 de noviembre de 2024]. Disponible en:
https://www.sciencedirect.com/topics/mathematics/population-correction-factor
10. Hajian-Tilaki K. Sample size estimation in diagnostic test
studies of biomedical informatics. J Biomed Inform. [Internet].2014 [Consultado el 3 de noviembre de
2024];48:193-204. doi:10.1016/j.jbi.2014.02.013
11. Lohr SL. Sampling: design and analysis. 2ª ed. Boston:
Mass: Brooks/Cole; 2010.
12. Kelley K.
Sample size planning for the coefficient of variation from the accuracy in
parameter estimation approach. Behav Res Methods
[Internet]. 2007 [Consultado el 3 de noviembre de 2024];39(4):755-66. doi:10.3758/BF03192966
13. Jones SR, Carley S, Harrison M. An introduction to power and sample
size estimation. Emerg Med J. [Internet]. 2003 [Consultado el 3 de noviembre de
2024];20(5):453-8. doi:10.1136/emj.20.5.453
14. Das S, Mitra K, Mandal M. Sample size calculation: Basic
principles. Indian J Anaesth. [Internet].
2016 [Consultado el 3 de noviembre de 2024];60(9):652-6.
doi:10.4103/0019-5049.190621
15. Anastasi
JK, Capili B, Norton M, McMahon DJ, Marder K. Recruitment and retention of clinical trial participants:
understanding motivations of patients with chronic pain and other populations.
Frontiers in Pain Research [Internet]. 2024 [Consultado
el 3 de noviembre de 2024];4:1330937.
doi:10.3389/fpain.2023.1330937
16. Smith PG,
Morrow RH, Ross DA. Field Trials of Health Interventions [Internet]. 3ª ed. Oxford: OUP Oxford; 2015 [Consultado el 3 de
noviembre de 2024]. Disponible en: http://www.ncbi.nlm.nih.gov/books/NBK305515/
ANEXOS
Anexo 1. Análisis logístico del
ejemplo 1
Anexo 2. Análisis logístico del
ejemplo 2
Anexo 3. Análisis logístico del
ejemplo 3